مدل‌سازی

کاربردهای مدل‌سازی برنامه‌ریزی خطی

برنامه‌ریزی خطی در صنایع و حوزه‌های مختلف کاربردهای متعددی دارد.

• در صنعت حمل‌ونقل، برای تعیین مسیر بهینه کامیون‌ها یا ناوگان حمل‌ونقل استفاده می‌شود تا هزینه‌های سوخت و زمان سفر به حداقل برسد. مثلاً یک شرکت پخش مواد غذایی می‌تواند با برنامه‌ریزی خطی مشخص کند که کدام مسیرها برای تحویل محصولات سریع‌تر و ارزان‌تر هستند.

• در حوزه تولید، یک کارخانه ممکن است با مسئله تخصیص منابع مواجه باشد؛ به عنوان مثال، می‌خواهد بداند چه تعداد از هر محصول را تولید کند تا سود خود را حداکثر کرده و در عین حال محدودیت‌های مربوط به مواد اولیه و نیروی کار را رعایت کند. در این حالت برنامه‌ریزی خطی کمک می‌کند تا ترکیب بهینه تولید مشخص شود.

• در بازارهای مالی، برنامه‌ریزی خطی برای بهینه‌سازی سبد سرمایه‌گذاری کاربرد دارد. یک مدیر مالی ممکن است بخواهد سرمایه خود را بین چندین نوع دارایی تقسیم کند به طوری که بازده کلی سبد بیشینه شود و در عین حال میزان ریسک از سطح مشخصی فراتر نرود.

• در کشاورزی، از این روش برای برنامه‌ریزی کشت استفاده می‌شود. مثلاً یک کشاورز با توجه به محدودیت آب و زمین در اختیار می‌تواند از برنامه‌ریزی خطی استفاده کند تا مشخص شود چه مقدار از هر محصول کاشته شود تا سود حاصله حداکثر شود.

• در بهداشت و درمان، بیمارستان‌ها از این روش برای زمان‌بندی جراحی‌ها و تخصیص منابع پزشکی مثل تخت‌های بیمارستانی استفاده می‌کنند تا بتوانند با کمترین زمان انتظار بیشترین تعداد بیماران را پوشش دهند. همچنین در مدیریت پروژه، به‌ویژه در پروژه‌های عمرانی، از برنامه‌ریزی خطی برای تخصیص منابع به فعالیت‌های مختلف و حداقل‌سازی زمان تکمیل پروژه استفاده می‌شود.

محدودیت‌های برنامه‌ریزی خطی

برنامه‌ریزی خطی با وجود کاربردهای گسترده، محدودیت‌هایی نیز دارد. یکی از اصلی‌ترین محدودیت‌ها این است که فرض می‌کند تمامی روابط بین متغیرها خطی هستند، در حالی که در دنیای واقعی بسیاری از مسائل ماهیت غیرخطی دارند. همچنین این روش نمی‌تواند به‌خوبی با داده‌های غیرقطعی یا شرایط پویا که در طول زمان تغییر می‌کنند، کنار بیاید. فرض دیگر آن است که تمامی پارامترها دقیق و قطعی هستند، در حالی که در عمل عدم قطعیت‌هایی مثل نوسانات قیمت یا تغییرات تقاضا وجود دارد.

مثلاً در کشاورزی، برنامه‌ریزی خطی فرض می‌کند که منابعی مثل آب یا کود کاملاً ثابت و قابل پیش‌بینی هستند، اما در واقعیت شرایط آب‌وهوایی می‌تواند پیش‌بینی‌ها را تغییر دهد. در حوزه تولید، اگر تقاضای بازار به طور ناگهانی تغییر کند، مدل بهینه‌سازی خطی نمی‌تواند به‌سرعت خود را با این تغییرات تطبیق دهد. در مدیریت پروژه نیز گاهی ارتباط بین فعالیت‌ها پیچیده و غیرخطی است، مانند تأخیرهای زنجیره‌ای که مدل خطی قادر به مدل‌سازی دقیق آن‌ها نیست. همچنین در مسائل مالی، این روش نمی‌تواند ریسک‌های غیرخطی یا اثرات نامطمئن بازار را به‌خوبی پیش‌بینی و مدیریت کند.

مثال‌های کاربردی مدل‌سازی برنامه‌ریزی خطی

مدل خطی دو متغیره

مثال تولید رنگ

یک کارخانه تولید رنگ دو نوع رنگ داخلی و خارجی تولید می‌کند که در آن‌ها از دو ماده اولیه استفاده می‌شود. جدول زیر جزئیات تولید هر محصول و مصرف مواد اولیه در آن را نشان می‌دهد. توجه داشته باشید که تقاضای بازار برای رنگ داخلی نمی‌تواند بیش از یک تن از تقاضای رنگ خارجی بیشتر باشد. همچنین، حداکثر تقاضای روزانه برای رنگ داخلی دو تن است. برنامه‌ریزی تولید رنگ‌های داخلی و خارجی را با هدف بیشینه‌سازی سود انجام دهید.

	رنگ خارجی	رنگ داخلی	ظرفیت روزانه انبار
مواد اولیه ۱	6	4	24
مواد اولیه ۲	1	2	6
سود در هر تن (هزار دلار)	5	4

متغیرهای مستقل

• \(x_1\): تولید رنگ خارجی
• \(x_2\): تولید رنگ داخلی

مدل

\[\begin{align} Maximize\ z = 5x_1 + 4x_2 \\ \\ subject\ to \\ 6x_1 + 4x_2 \leq 24 \\ x_1 + 2x_2 \leq 6 \\ x_2 - x_1 \leq 1 \\ x_2 \leq 2 \\ \\ x_1, x_2 \geq 0 \\ \end{align}\]

حل ترسیمی

حل توسط اکسل

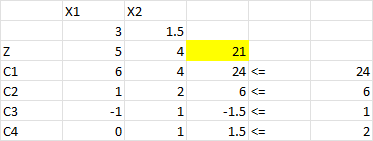
فعال‌سازی Solver در اکسل

مثال برنامه غذایی

یک کارخانه دامپروری روزانه ۸۰۰ پوند از یک ماده غذایی خاص استفاده می‌کند. این ماده غذایی مخلوطی از سویا و ذرت با ترکیبات زیر است.

ماده غذایی	پروتئین	فیبر	هزینه
ذرت	0.09	0.02	0.30
سویا	0.60	0.06	0.90

طبق الزامات استاندارد این ماده غذایی بایستی شامل حداقل ۳۰ درصد پروتئین و حداکثر ۵ درصد فیبر باشد. طرح اختلاط بهینه را تعیین کنید.

متغیرهای مستقل

• ذرت: \(x_1\)
• سویا: \(x_2\)

مدل

\[\begin{align} Minimize\ z = .3x_1 + .9x_2 \\ \\ subject\ to \\ x_1 + x_2 \geq 800 \\ .09x_1 + .6x_2 \geq .3(x_1 + x_2) \\ .02x_1 + .06x_2 \leq .05(x_1 + x_2) \\ \\ x_1,x_2 \geq 0 \end{align}\]

حل ترسیمی

حل توسط اکسل

مدل خطی چند متغیره

مثال سیاست گذاری وام بانکی

یک بانک در پی طراحی یک سیاست جدید اعطای وام به مبلغ حداکثر ۱۲ میلیون دلار است. مشخصات انواع وام این طرح در جدول زیر ارائه شده است

نوع وام	نرخ بهره	بدحسابی
شخصی	0.140	0.10
اتومبیل	0.130	0.07
مسکن	0.120	0.03
کشاورزی	0.125	0.05
کسب و کار	0.100	0.02

بدحسابی غیرقابل برگشت بوده و درآمدی از بهره ایجاد نمی‌کند. شرایط رقابتی ایجاب می‌کند که حداقل ۴۰ درصد از وام به کشاورزی و کسب و کار تخصیص یابد. برای کمک به صنعت مسکن بومی وام مسکن بایستی حداقل ۵۰ درصد وام شخصی و خودرو و مسکن باشد. مقدار کل بدحسابی نبایستی از ۴ درصد بیشتر باشد.

متغیرهای مستقل

• \(x_1\): وام شخصی
• \(x_2\): اتومبیل
• \(x_3\): مسکن
• \(x_4\): کشاورزی
• \(x_5\): کسب و کار

مدل

• بهره کل = \(.14(.9x_1) + .13(.93x_2) + .12(.97x_3) + .125(.95x_4) + .1 (.98x_5)\)
• بد حسابی = \(.1x_1 + .07x_2 + .03x_3 + .05x_4 + .02x_5\)

\[\begin{align} Maximize\ z = .14(.9x_1) + .13(.93x_2) + .12(.97x_3) + .125(.95x_4) + .1 (.98x_5) \\ - (.1x_1 + .07x_2 + .03x_3 + .05x_4 + .02x_5) \\ \\ subject\ to \\ x_1 + x_2 + x_3 + x_4 + x_5 \leq 12 \\ x_4 + x_5 \geq .4(x_1 + x_2 + x_3 + x_4 + x_5) \\ x_3 \geq .5(x_1 + x_2 + x_3) \\ .1x_1 + .07x_2 + .03x_3 + .05x_4 + .02x_5 \leq .04(x_1 + x_2 + x_3 + x_4 + x_5) \\ \\ x_1, x_2, x_3, x_4, x_5 \geq 0 \end{align}\]

حل توسط اکسل

مثال برنامه‌ریزی کنترل و انبار

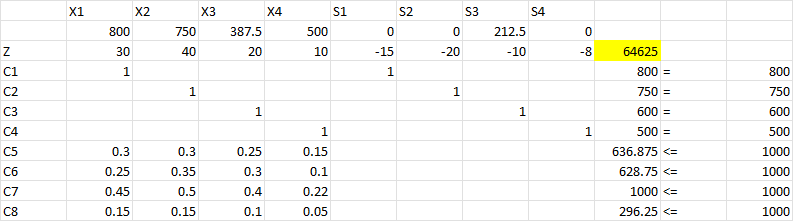
در تدارک فصل زمستان یک شرکت تولید پوشاک، کاپشن، کت، شلوار و دستکش تولید می‌کند. همه محصولات چهار مرحله برش، آستر، دوخت و بسته‌بندی را طی می‌کنند. این شرکت یک قرارداد تولید بسته که مشخصات آن به قرار جدول زیر است. در این قرارداد به ازای عدم تحویل هر یک از اقلام جریمه در نظر گرفته شده است. برنامه بهینه تولید را بنویسید.

مرحله	کاپشن	کت	شلوار	دستکش	ظرفیت
برش (ساعت)	0.30	0.30	0.25	0.15	1000
آستر (ساعت)	0.25	0.35	0.30	0.10	1000
دوخت (ساعت)	0.45	0.50	0.40	0.22	1000
بسته‌بندی (ساعت)	0.15	0.15	0.10	0.05	1000
سفارش (عدد)	800	750	600	500
سود (دلار)	30	40	20	10
جریمه (دلار)	15	20	10	8

متغیرهای مستقل

• \(x_1\): تعداد تولید کاپشن
• \(x_2\): تعداد تولید کت
• \(x_3\): تعداد تولید شلوار
• \(x_4\): تعداد تولید دستکش
• \(s_1\): جریمه کسری کاپشن
• \(s_2\): جریمه کسری کت
• \(s_3\): جریمه کسری شلوار
• \(s_4\): جریمه کسری دستکش

مدل

• سود خالص = سود کل - جریمه کل
• سود کل = \(30x_1 + 40x_2 + 20x_3 + 10x_4\)
• جریمه کل = \(15s_1 + 20s_2 + 10s_3 + 8s_4\)

\[\begin{align} Maximize\ z = 30x_1 + 40x_2 + 20x_3 + 10x_4 \\ - (15s_1 + 20s_2 + 10s_3 + 8s_4) \\ \\ subject\ to \\ x_1 + s_1 = 800 \\ x_2 + s_2 = 750 \\ x_3 + s_3 = 600 \\ x_4 + s_4 = 500 \\ .30x_1 + .30x_2 + .25x_3 + .15x_4 \leq 1000 \\ .25x_1 + .35x_2 + .30x_3 + .10x_4 \leq 1000 \\ .45x_1 + .50x_2 + .40x_3 + .22x_4 \leq 1000 \\ .15x_1 + .15x_2 + .10x_3 + .05x_4 \leq 1000 \\ \\ x_1, x_2, x_3, x_4, s_1, s_2, s_3, s_4 \geq 0 \end{align}\]

حل توسط اکسل

مثال برنامه‌ریزی تولید پنجره

یک شرکت ساخت پنجره قرار است در شش ماه آینده ۱۰۰، ۲۵۰، ۱۹۰، ۱۴۰، ۲۲۰ و ۱۱۰ پنجره بسازد. هزینه تولید که شامل کارگر مصالح و تجهیزات است در شش ماه آینده به ترتیب برابر با ۵۰، ۴۵، ۵۵، ۴۸، ۵۲ و ۵۰ دلار به ازای هر پنجره می‌باشد. این شرکت می‌تواند در یک ماه بیش از میزان تقاضا تولید نموده و آن را در انبار ذخیره کرده و در ماه‌های بعد تحویل دهد. هزینه انبارش به ازای هر پنجره ۸ دلار در ماه می‌باشد. برنامه تولید بهینه را بنویسید.

جدول داده‌ها

ماه	1	2	3	4	5	6
هزینه تولید	50	45	55	48	52	50
هزینه انبار	8	8	8	8	8	8
تعداد سفارش	100	250	190	140	220	110

متغیرهای مستقل

• \(x_i\): تعداد تولید در ماه \(i\)
• \(s_i\): تعداد انبار در ماه \(i\)

مدل

• هزینه کل = هزینه تولید + هزینه انبار
• هزینه تولید = \(50x_1 + 45x_2 + 55x_3 + 48x_4 + 52x_5 + 50x_6\)
• هزینه انبار = \(8(s_1 + s_2 + s_3 + s_4 + s_5 + s_6)\)

\[\begin{align} Minimize\ z = 50x_1 + 45x_2 + 55x_3 + 48x_4 + 52x_5 + 50x_6 \\ + 8(s_1 + s_2 + s_3 + s_4 + s_5 + s_6) \\ \\ subject\ to \\ x_1 - s_1 = 100 \\ s_1 + x_2 - s_2 = 250 \\ s_2 + x_3 - s_3 = 190 \\ s_3 + x_4 - s_4 = 140 \\ s_4 + x_5 - s_5 = 220 \\ s_5 + x_6 - s_6 = 110 \\ \\ x_i, s_i \geq 0; \forall i \in \{1, 2, ..., 6\} \end{align}\]

حل توسط اکسل

مثال برنامه‌ریزی منابع انسانی

یک کارخانه در صدد تولید یک محصول برای چهار ماه آینده است. تعداد سفارش این محصول به ترتیب ۵۲۰، ۷۲۰، ۵۲۰ و ۶۲۰ واحد می‌باشد. این شرکت دارای ۱۰ کارگر ثابت می‌باشد لیکن بنا به نیاز تولید می‌تواندکارگر موقت استخدام یا اخراج کند. هزینه استخدام و اخراج به ترتیب ۲۰۰ و ۴۰۰ دلار می‌باشد. هر کارگر دائم ۱۲ واحد و هر کارگر موقت ۱۰ واحد در ماه تولید می‌کند. این شرکت می‌تواند بیش از مقدار سفارش در ماه تولید نموده و هر واحد باقیمانده را با هزینه ۵۰ دلار در ماه انبار کند. سیاست استخدام و اخراج بهینه را برای چهارماه آینده برنامه‌ریزی کنید.

جدول داده‌ها

	ماه ۱	ماه ۲	ماه ۳	ماه ۴
سفارش	520	720	520	620
هزینه انبار $	50	50	50	50

متغیرها

• \(s_i\): تعداد انبار در ماه \(i\)
• \(h_i\): تعداد استخدام در ماه \(i\)
• \(f_i\): تعداد اخراج در ماه \(i\)

مدل

• هزینه کل = هزینه تولید + هزینه انبار
• هزینه تولید = \(200(h_1 + h_2 + h_3 + h_4) + 400(f_1 + f_2 + f_3 + f_4)\)
• هزینه انبار = \(50(s_1 + s_2 + s_3 + s_4)\)

\[\begin{align} Minimize\ z = 200(h_1 + h_2 + h_3 + h_4) \\ + 400(f_1 + f_2 + f_3 + f_4) \\ + 50(s_1 + s_2 + s_3 + s_4) \\ \\ subject\ to \\ 10(h_1 - f_1) = 400 + s_1 \\ s_1 + 10(h_1 + h_2 - f_1 - f_2) = 600 + s_2 \\ s_2 + 10(h_1 + h_2 + h_3 - f_1 - f_2 - f_3) = 400 + s_3 \\ s_3 + 10(h_1 + h_2 + h_3 + h_4 - f_1 - f_2 - f_3 - f_4) = 500 + s_4 \\ \\ x_i, s_i, h_i, f_i \geq 0; \forall i \in \{1, 2, 3, 4\} \end{align}\]

حل توسط اکسل

مثال برنامه‌ریزی حمل و نقل

شهرداری یک شهر قصد دارد یک طرح اتوبوسرانی عمومی را برای کاهش استفاده از خودروهای شخصی برنامه‌ریزی کند. هدف این طرح پیدا کردن حداقل تعداد ناوگان اتوبوسی است که بتواند نیازهای حمل و نقل را پوشش دهد. نتیجه مطالعات و جمع آوری اطلاعات نشان داد که حداقل تعداد اتوبوس مورد نیاز برای حمل و نقل مسافر در بازه‌های ۴ ساعته، الگویی مشابه شکل زیر دارد. در صورتی که هر اتوبوس حداکثر ۸ ساعت در روز قادر به سرویس دهی باشد، حداقل تعداد اتوبوس مورد نیاز در هر بازه زمانی را مشخص کنید.

متغیرهای مستقل

• \(x_1\): تعداد اتوبوس‌ها از ۱۲ بامداد\(i\)
• \(x_2\): تعداد اتوبوس‌ها از ۴ صبح\(i\)
• \(x_3\): تعداد اتوبوس‌ها از ۸ صبح\(i\)
• \(x_4\): تعداد اتوبوس‌ها از ۱۲ ظهر\(i\)
• \(x_5\): تعداد اتوبوس‌ها از ۴ بعد از ظهر\(i\)
• \(x_6\): تعداد اتوبوس‌ها از ۸ بعد از ظهر\(i\)

مدل

• تعداد کل اتوبوس‌ها = جمع تعداد اتوبوس در بازه‌های زمانی

\[\begin{align} Minimize\ z = x_1 + x_2 + x_3 + x_4 + x_5 + x_6 \\ \\ subject\ to \\ x_1 + x_2 \geq 8 \\ x_2 + x_3 \geq 10 \\ x_3 + x_4 \geq 7 \\ x_4 + x_5 \geq 12 \\ x_5 + x_6 \geq 4 \\ x_1 + x_6 \geq 4 \\ \\ x_i \geq 0; x \in \{1, 2, ..., 6\} \end{align}\]

حل توسط اکسل

مثال برنامه‌ریزی شهری

شورای برنامه‌ریزی یک شهر با کمبود بودجه مواجه شده است. برنامه شورا برای جبران کسری بودجه این است که ساختمان‌های قدیمی را با ساختمان‌های مدرن جایگزین کرده و از درآمد مالیاتی آن بهره بگیرد. این پروژه شامل دو مرحله است

• تخریب ساختمان‌های قدیمی و غیر استاندارد برای فراهم آوردن فضای کافی جهت توسعه
• ساخت ساختمان‌های جدید با در نظر گرفتن شرایط زیر
• ۳۰۰ ساختمان قدیمی می‌تواند تخریب شده که مساحت هر کدام از آنها 0.25 جریب می‌باشد. هزینه تخریب هر ساختمان ۲۰۰۰ دلار است.
• مساحت ساختمان‌های جدید تک، دو، سه و چهار نفره به ترتیب برابر با 0.18، 0.28، 0.40 و 0.50 جریب می‌باشد. ۱۵ درصد از کل فضای جدید برای خیابان‌ها و فضاهای باز در نظر گرفته شده است.
• حداقل ۲۵ درصد از کل ساختمان‌های جدید بایستی به خانه‌های سه و چهار نفره تخصیص یابد. خانه‌های تک و دو نفره بایستی حداقل به ترتیب ۲۰ و ۱۰ درصد کل ساخت و ساز را دربرگیرد.
• مالیات دریافتی برای خانه‌های تک، دو، سه و چهار نفره به ترتیب ۱۰۰۰، ۱۹۰۰، ۲۷۰۰ و ۳۴۰۰ دلار می‌باشد.
• هزینه ساخت برای خانه‌های تک، دو، سه و چهار نفره به ترتیب ۵۰، ۷۰، ۱۳۰ و ۱۶۰ هزار دلار می‌باشد.
• کل وام قابل دریافت از بانک محلی ۱۵ میلیون دلار است.

از هر واحد چه تعداد ساخته شود تا بتوان بیشترین درآمد مالیاتی را کسب کرد؟

جدول داده‌ها

	تک نفره	دو نفره	سه نفره	چهار نفره
مساحت ساختمان	0.18	0.28	0.40	0.50
مالیات قابل دریافت (دلار)	1000	1900	2700	3400
هزینه ساخت (هزار دلار)	50	70	130	160

متغیرهای مستقل

• تعداد ساختمان تک نفره: \(x_1\)
• تعداد ساختمان دو نفره: \(x_2\)
• تعداد ساختمان سه نفره: \(x_3\)
• تعداد ساختمان چهار نفره: \(x_4\)
• تعداد ساختمان‌هایی که بایستی تخریب: \(x_5\)

مدل

\[\begin{align} Maximize\ z = 1000x_1 + 1900x_2 + 2700x_3 + 3400x_4 \\ \\ subject\ to \\ .18x_1 + .28x_2 + .40x_3 + .50x_4 \leq (.85 \times .25)x_5 \\ x_5 \leq 300 \\ x_1 \geq .2(x_1 + x_2 + x_3 + x_4) \\ x_2 \geq .1(x_1 + x_2 + x_3 + x_4) \\ x_3 + x_4 \geq .25(x_1 + x_2 + x_3 + x_4) \\ 50x_1 + 70x_2 + 130x_3 + 160x_4 + 2x_5 \leq 15,000 \\ \\ x_i \geq 0; \forall i \in \{1,2, ..., 5\} \end{align}\]

حل توسط اکسل

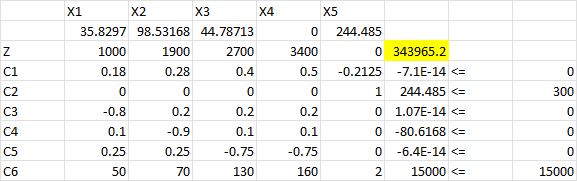
مثال پالایشگاه نفت

یک پالایشگاه با ظرفیت یک و نیم میلیون بشکه نفت خام در روز سه نوع سوخت معمولی، پرمیوم و سوپر با اعداد اکتان ۸۷، ۸۹ و ۹۲ تولید می‌کند. فرایند پالایش شامل سه مرحله زیر است:

1. برج تقطیر نفت خام را گرفته و یک میان محصول با عدد اکتان ۸۲ و با نرخ ۲۰ درصد تولید می‌کند.
2. واحد شکست با ظرفیت ورودی ۲۰۰ هزار بشکه، میان محصول را گرفته و سوخت با عدد اکتان ۹۸ و با نرخ ۵۰ درصد تولید می‌کند.
3. واحد اختلاط خروجی دو واحد قبل را گرفته و با نسبت‌های مختلف سه نوع سوخت با عدد اکتان فوق را تولید می‌کند.

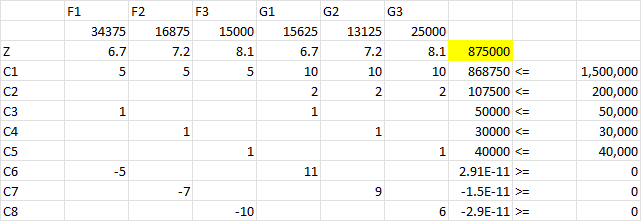
سود هر یک از سوخت‌های فوق به ترتیب 6.7، 7.2 و 8.1 دلار در بشکه می‌باشد. تقاضای روزانه برای محصولات این پالایشگاه به ترتیب ۵۰، ۳۰ و ۴۰ هزار بشکه در روز می‌باشد. برنامه بهینه تولید را برای این پالایشگاه بنویسید.

جدول داده‌ها

	معمولی	پرمیوم	سوپر
عدد اکتان	87	89	92
سود (دلار در بشکه)	6.7	7.2	8.1
تقاضا (هزار بشکه)	50	30	40

متغیرها

• مقدار تولید سوخت 1: \(x_1 = f_1 + g_1\)
• مقدار تولید سوخت 2: \(x_2 = f_2 + g_2\)
• مقدار تولید سوخت 3: \(x_3 = f_3 + g_3\)

مدل

\[\begin{align} Maximize\ z = 6.7(f_1 + g_1) + 7.2(f_2 + g_2) + 8.1(f_3 + g_3) \\ \\ subject\ to \\ 5[f_1 + f_2 + f_3 + 2(g_1 + g_2 + g_3)] \leq 1,500,000 \\ 2(g_1 + g_2 + g_3) \leq 200,000 \\ f_1 + g_1 \leq 50,000 \\ f_2 + g_2 \leq 30,000 \\ f_3 + g_3 \leq 40,000 \\ \frac{82f_1 + 98g_1}{f_1 + g_1} \geq 87 \\ \frac{82f_2 + 98g_2}{f_2 + g_2} \geq 89 \\ \frac{82f_3 + 98g_3}{f_3 + g_3} \geq 92 \\ \\ f_i,g_i \geq 0; \forall i \in \{1, 2, 3\} \end{align}\]

حل توسط اکسل

تمرین‌های تکمیلی

تمرین فضای جواب

فضای جواب را برای هریک از قیود زیر مشخص کنید

• \(-3x_1 + x_2 \leq 6\)
• \(x_1 - 2x_2 \geq 5\)
• \(2x_1 - 3x_2 \leq 12\)
• \(x_1 - x_2 \leq 0\)
• \(-x_1 + x_2 \geq 0\)

تمرین تابع هدف

• \(Maxizmize\ z = x_1 - x_2\)
• \(Maxizmize\ z = -8x_1 - 3x_2\)
• \(Maxizmize\ z = -x_1 + 3x_2\)
• \(Maxizmize\ z = -3x_1 + x_2\)

تمرین برنامه‌ریزی تولید

یک شرکت روزانه دو نوع محصول را طی سه مرحله تولید می‌کند که برای تولید آنها ۱۰ ساعت در روز زمان صرف می‌کند. سود هر محصول و زمان مورد نیاز برای تولید در هر مرحله (به دقیقه) در جدول زیر ارائه شده است. برنامه‌ریزی تولید بهینه را بنویسید.

محصول	مرحله ۱	مرحله ۲	مرحله ۳	سود (دلار)
۱	۱۰	۶	۸	۲۰
۲	۵	۲۰	۱۰	۳۰

تمرین چیدمان قفسه

در یک فروشگاه کوچک مصالح ساختمانی، فضای قفسه محدود است و باید به بهترین نحو از آن استفاده شود تا سود افزایش یابد. دو نوع مصالح گچ و سیمان برای اشغال کل 60 فوت مربع فضای قفسه رقابت می‌کنند. هر پاکت گچ 0.2 فوت مربع و هر پاگت سیمان 0.4 فوت مربع فضا اشغال می‌کند. حداکثر تقاضای روزانه برای سیمان 200 پاکت و برای سیمان 120 پاکت است. هر پاکت گچ 1 دلار و هر پاکت سیمان 1.35 دلار سود دارد. صاحبان فروشگاه فکر می‌کنند چون سود واحد سیمان 35 درصد بیشتر از گچ است، پس باید 35 درصد فضای بیشتری به آن اختصاص دهند؛ یعنی حدود 57 درصد فضا به سیمان و 43 درصد به گچ. نظر شما چیست؟

تمرین برنامه‌ریزی تحصیلی

جک یک دانشجوی تازه‌وارد در دانشگاه است. او متوجه شده که «فقط کار کردن و بازی نکردن برای او کسل‌کننده است.» بنابراین او می‌خواهد حدود 10 ساعت از وقت روزانه‌اش را بین کار و تفریح تقسیم کند. او برآورد کرده که تفریح کردن دو برابر کار کردن لذت‌بخش است. همچنین قصد دارد حداقل به اندازه‌ای که تفریح می‌کند، مطالعه هم داشته باشد. با این حال، جک می‌داند که برای انجام تمام تکالیفش نمی‌تواند بیش از 4 ساعت در روز تفریح کند. جک چگونه باید زمانش را تخصیص دهد تا بیشترین لذت را از هر دو فعالیت ببرد؟

تمرین برنامه‌ریزی تولید مبلمان منزل

یک شرکت مبلمان، میز و صندلی تولید می‌کند. بخش برش‌کاری، چوب را برای هر دو محصول برش می‌دهد که سپس به بخش‌های مونتاژ جداگانه فرستاده می‌شود. اقلام مونتاژ شده برای تکمیل نهایی به بخش رنگ‌آمیزی فرستاده می‌شوند. ظرفیت روزانه بخش برش‌کاری ۲۰۰ صندلی یا ۸۰ میز است. بخش مونتاژ صندلی می‌تواند روزانه ۱۲۰ صندلی تولید کند و بخش مونتاژ میز روزانه ۶۰ میز تولید می‌کند. بخش رنگ‌آمیزی ظرفیت روزانه ۱۵۰ صندلی یا ۱۱۰ میز را دارد. با توجه به اینکه سود هر صندلی ۵۰ دلار و سود هر میز ۱۰۰ دلار است، ترکیب بهینه تولید برای شرکت را تعیین کنید.

تمرین حل ترسیمی

مدل زیر را به روش ترسیمی حل کنید

\[\begin{align} Minimize\ z = 3x_1 + 8x_2\\ \\ x_1 + x_2 \geq 8 \\ 2x_1 - 3x_2 \leq 0 \\ x_1 + 2x_2 \leq 30 \\ 3x_1 - x_2 \geq 0 \\ x_1 \leq 10 \\ x_2 \geq 9 \\ \\ x_1,x_2 \geq 0 \end{align}\]

تمرین قیود موازی

مدل زیر را ترسیم کنید و قیود موازی را مشخص کنید

\[\begin{align} Maximize\ z = 5x_1 + 4x_2\\ \\ 6x_1 + 4x_2 \leq 24 \\ 6x_1 + 3x_2 \leq 22.5 \\ x_1 + x_2 \leq 5 \\ x_1 + 2x_2 \leq 6 \\ -x_1 + x_2 \leq 1 \\ x_2 \leq 2 \\ \\ x_1, x_2 \geq 0 \end{align}\]

افزودن قید \(x_2 \geq 3\) چه تغییری در فضای جواب ایجاد می‌کند؟

تمرین برنامه‌ریزی تولید محصولات نفتی

یک شرکت نفتی در حال ساخت پالایشگاهی برای تولید چهار محصول است: دیزل، بنزین، روان‌کننده‌ها و سوخت جت. حداقل تقاضا (بر حسب بشکه در روز) برای هر یک از این محصولات به ترتیب ۱۴٬۰۰۰، ۳۰٬۰۰۰، ۱۰٬۰۰۰ و ۸٬۰۰۰ است. عراق و دبی قرارداد ارسال نفت خام به شرکت نفت را دارند. به دلیل سهمیه‌های تولید مشخص شده توسط اوپک (سازمان کشورهای صادرکننده نفت)، پالایشگاه جدید باید حداقل ۴۰٪ نفت خام خود را از عراق و مابقی را از دبی دریافت کند. شرکت نفت پیش‌بینی می‌کند که تقاضا و سهمیه‌های نفت خام طی ۱۰ سال آینده ثابت باقی خواهد ماند. مشخصات دو نوع نفت خام منجر به ترکیب‌های محصول متفاوتی می‌شود. یک بشکه نفت خام عراق ۰.۲ بشکه دیزل، ۰.۲۵ بشکه بنزین، ۰.۱ بشکه روان‌کننده و ۰.۱۵ بشکه سوخت جت تولید می‌کند. بازده متناظر از نفت خام دبی به ترتیب ۰.۱، ۰.۶، ۰.۱۵ و ۰.۱ است. حداقل ظرفیت پالایشگاه (بر حسب بشکه در روز) را تعیین کنید.

تمرین برنامه‌ریزی ساخت و ساز

یک شرکت ساختمانی شش پروژه را برای ساخت و ساز طی چهار سال آینده در نظر گرفته است. این شرکت می‌تواند هر یک از پروژه‌ها را به صورت جزئی یا کامل اجرا کند. اجرای جزئی یک پروژه، هم بازده و هم هزینه‌های نقدی را به طور متناسب محاسبه خواهد کرد. بازده مورد انتظار (ارزش فعلی) و هزینه‌های نقدی برای پروژه‌ها در جدول زیر آمده است.

پروژه	هزینه سال ۱ (هزار دلار)	هزینه سال ۲ (هزار دلار)	هزینه سال ۳ (هزار دلار)	هزینه سال ۴ (هزار دلار)	بازده (هزار دلار)
۱	۱۰٫۵	۱۴٫۴	۲٫۲	۲٫۴	۳۲۴٫۰۰
۲	۸٫۳	۱۲٫۶	۹٫۵	۳٫۱	۳۵۸٫۰۰
۳	۱۰٫۲	۱۴٫۲	۵٫۶	۴٫۲	۱۷۷٫۵۰
۴	۷٫۲	۱۰٫۵	۷٫۵	۵٫۰	۱۴۸٫۰۰
۵	۱۲٫۳	۱۰٫۱	۸٫۳	۶٫۳	۱۸۲٫۰۰
۶	۹٫۲	۷٫۸	۶٫۹	۵٫۱	۱۲۳٫۵۰
منابع مالی موجود (هزار دلار)	۶۰٫۰	۷۰٫۰	۳۵٫۰	۲۰٫۰	-

• مسئله را به صورت یک برنامه خطی فرمول‌بندی کنید و ترکیب بهینه پروژه که بازده کل را حداکثر می‌کند را با استفاده از اکسل تعیین کنید. ارزش زمانی پول را نادیده بگیرید.
• فرض کنید اگر بخشی از پروژه ۲ انجام شود، حداقل باید بخش برابری از پروژه ۶ نیز انجام شود. فرمول‌بندی مدل را اصلاح کنید و راه‌حل بهینه جدید را پیدا کنید.
• در مدل اصلی، فرض کنید هر مقدار پولی که در پایان سال باقی می‌ماند در سال بعد استفاده می‌شود. راه‌حل بهینه جدید را پیدا کنید و تعیین کنید که هر سال چه مقدار از سال قبل "قرض می‌گیرد". برای سادگی، ارزش زمانی پول را نادیده بگیرید.
• فرض کنید در مدل اصلی، بودجه سالانه موجود برای هر سال را می‌توان در صورت لزوم با قرض گرفتن از سایر فعالیت‌های مالی درون شرکت افزایش داد. با نادیده گرفتن ارزش زمانی پول، مدل LP را دوباره فرمول‌بندی کنید و راه‌حل بهینه را پیدا کنید. آیا راه‌حل جدید در هر سال نیاز به قرض گرفتن دارد؟ اگر بله، نرخ بازده پول قرض گرفته شده چقدر است؟

تمرین برنامه‌ریزی ساخت و ساز

شهر فایتویل در حال آغاز یک پروژه نوسازی شهری است که شامل خانه‌های ردیفی برای اقشار کم‌درآمد و متوسط، آپارتمان‌های لوکس برای اقشار پردرآمد و مسکن عمومی خواهد بود. این پروژه همچنین شامل یک مدرسه ابتدایی دولتی و امکانات خرده‌فروشی است. اندازه مدرسه ابتدایی (تعداد کلاس‌ها) متناسب با تعداد دانش‌آموزان است و فضای خرده‌فروشی متناسب با تعداد واحدهای مسکونی است. جدول زیر اطلاعات مربوط به این وضعیت را ارائه می‌دهد.

	درآمد پایین	درآمد متوسط	درآمد بالا	مسکن عمومی	اتاق مدرسه	واحد خرده‌فروشی
حداقل تعداد واحدها	۱۰۰	۱۲۵	۷۵	۳۰۰		۰
حداکثر تعداد واحدها	۲۰۰	۱۹۰	۲۶۰	۶۰۰		۲۵
اندازه زمین به ازای هر واحد (جریب)	۰.۰۵	۰.۰۷	۰.۰۳	۰.۰۲۵	۰.۰۴۵	۰.۱
میانگین تعداد دانش‌آموز در هر واحد	۱.۳	۱.۲	۰.۵	۱.۴
تقاضای خرده‌فروشی به ازای هر واحد (جریب)	۰.۰۲۳	۰.۰۳۴	۰.۰۴۶	۰.۰۲۳	۰.۰۳۴
درآمد سالیانه به ازای هر واحد (دلار)	۷,۰۰۰	۱۲,۰۰۰	۲۰,۰۰۰	۵,۰۰۰	-	۱۵,۰۰۰

مدرسه جدید می‌تواند حداکثر ۲ جریب فضا اشغال کند. ظرفیت هر کلاس به ۲۵ دانش‌آموز در هر اتاق محدود است. هزینه سالانه عملیاتی برای هر کلاس ۱۰,۰۰۰ دلار است. این پروژه در یک زمین خالی ۵۰ جریبی متعلق به شهر واقع خواهد شد. علاوه بر این، پروژه می‌تواند از یک ملک مجاور که شامل ۲۰۰ خانه زاغه‌نشین تخریبی است استفاده کند. هر خانه تخریبی ۰.۲۵ جریب را اشغال می‌کند. هزینه خرید و تخریب هر واحد زاغه‌نشین ۷,۰۰۰ دلار است. فضای باز، خیابان‌ها و پارکینگ‌ها ۱۵٪ از کل زمین موجود را مصرف می‌کنند. یک برنامه خطی برای تعیین طرح بهینه پروژه تدوین کنید و با استفاده از اکسل پاسخ را پیدا کنید.

تمرین برنامه‌ریزی کنترل ترافیک

در یک تقاطع بزرگراهی، خودروهای خروجی از سه بزرگراه H1، H2 و H3 باید توقف کرده و برای ورود به عوارضی منتظر چراغ سبز بمانند. عوارض برای خودروهای خروجی از H1، H2 و H3 به ترتیب ۴، ۵ و ۶ دلار است. نرخ جریان از H1، H2 و H3 به ترتیب ۵۵۰، ۶۵۰ و ۴۵۰ خودرو در ساعت است. چرخه چراغ راهنمایی نباید از ۲.۲ دقیقه تجاوز کند و چراغ سبز در هر بزرگراه باید حداقل ۲۲ ثانیه باشد. چراغ زرد به مدت ۱۰ ثانیه روشن است. دروازه عوارضی می‌تواند حداکثر ۵۰۰ خودرو در ساعت را پردازش کند. با فرض اینکه هیچ خودرویی در زمان چراغ زرد حرکت نمی‌کند، فاصله زمانی بهینه چراغ سبز برای سه بزرگراه را تعیین کنید که درآمد دروازه عوارضی را در هر چرخه ترافیکی به حداکثر برساند.

تمرین بهینه‌سازی بارگذاری

یک جرثقیل سقفی با ابعاد و مشخصات زیر داده شده است. مقاومت حداکثر تکیه‌گاه‌ها ۲۵ کیلوپوند و مقاومت کابل‌ها ۲۰ کیلوپوند است. حدکثر بار \(W_2\) و \(W_1\) را محاسبه کنید.